 A recent working paper from the Bank of England reports on efforts to understand the rise of high-frequency trading and its impact on equity markets. I think it fair to say that the study fails to get any firm grasp of its subject matter, going “about it and about but evermore,” as poet Omar Khayyam wrote. The authors leave the subject by the same ambivalent door they used on the way in. Nonetheless, the trip is instructional, if only of the difficulties inherent in the subject matter.
A recent working paper from the Bank of England reports on efforts to understand the rise of high-frequency trading and its impact on equity markets. I think it fair to say that the study fails to get any firm grasp of its subject matter, going “about it and about but evermore,” as poet Omar Khayyam wrote. The authors leave the subject by the same ambivalent door they used on the way in. Nonetheless, the trip is instructional, if only of the difficulties inherent in the subject matter.
The authors – Evangelos Benos and Satchit Sagade – distinguish between aggressive HFTs (which take liquidity from the marketplace) and passive HFTs (which serve a market making function, providing liquidity). The aggressive HFTs as so defined are the more controversial figures in the HFT world, so one of Benos and Sagade’s concerns is to determine the difference that this difference makes.
In the chart below the passives are represented by the green line, aggressives by red, and all other traders by blue. (The dotted lines represent confidence bands.)
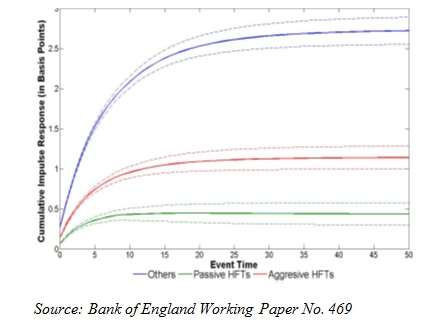
The graph is designed to show the price impact that the various sorts of traders have.
From Liquidity to Volatility
It appears that the aggressive HFTs have a larger impact than do the passive. One could rather hastily interpret this to mean that the aggressive HFTs make more of a contribution to price discovery than the passive HFTs. Aha! Then they are serving a function, and their price- discovery value justifies the liquidity they soak up. But wait ….
That inference would be too hasty because as Benos and Sagade also tell us, the larger contribution of the aggressives “is roughly proportional to their larger aggressively executed trading volume,” so that on a trade-by-trade basis, they aren’t really more informative than are the market makers after all.
There is no firm conclusion to be drawn from studying liquidity, so, let’s talk about volatility. Here, too, the authors start with a distinction. There is “good” volatility and there is “excessive” volatility (respectively, information and noise). They ask what HFT does to both.
A given trader can of course contribute to both. For example, the authors say, half of a particular party’s trades might be informed speculation (contributing to the information value of prices) while the other half are simply “used to calibrate her inventory levels,” adding to the level of noise.
Adding Hasbrouck to the Mix
The authors work from a formula proposed by Joel Hasbrouck in 1991:
pt = pt* + st.
In English prose: they assume with Hasbrouck both a random walk component (p*) reflecting the efficient information-discounted price and a stationary component (s) reflecting noise. The price at any given time (t) is the sum of both.
What does HFT do to s? The answer, again, is ambivalence. On the one hand, the high frequency traders have a higher information-to-noise ratio than old-fashioned human velocity traders. The HFTs in the database employed by these authors participated in only about 27 percent of the total traded volume but contributed “more than half of the total private information that is impounded in prices via trades.”
On the other hand, they also observe that “there are instances where HFTs contribute significantly more noise than the rest of the traders,” and where the aggressive group contributes a good deal more noise than the passive one within the HFT domain.
One reason for this is that HFTs typically want to end the day with their positions flat. This may require a lot of uninformed or noisy trades toward the end of a trading session.
The conclusion of all this is … no conclusion. “[The] overall welfare implications of HFT are unclear; these will depends on how the marginal benefit of information at some times compares with the marginal cost of excess volatility at other times, including in periods of market stress.”
Benos is a Bank of England Research Economist. Co-author Sagade is a Ph.D. candidate at the ICMA Centre, in Reading.



