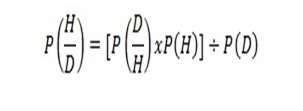 A surprising dust-up in the blogosphere in recent days concerns Thomas Bayes, and the distinctive branch of probability theory called “Bayesian” in his honor.
A surprising dust-up in the blogosphere in recent days concerns Thomas Bayes, and the distinctive branch of probability theory called “Bayesian” in his honor.
This has everything to do with the search for alpha. After all, probability is a key element in asset valuation. Consider the question “what is the probability that there is a lot of crude oil beneath this piece of land?” The way we go about answering that question: indeed, the way we go about understanding that question, depends upon whether we are Bayesians.
Further, in finance Bayes’ mid 18th century work has received a boost from a late 19th century Russian, Andrei Markov, so that the movements of asset prices, or the changing probabilities of default, or other variables are often modeled as “Bayesian-Markov chains.” This concept overlaps, but is distinct from, the idea of a random walk.
One Australian scholar has even made the case that a proper understanding of Bayesian probability theory raise questions about CAPM itself.
So the stakes are pretty high, and my ears pricked up recently when I heard of a sweeping challenge to the value of Bayesianism. As a Bayesian myself, I’ll try to describe this challenge fairly, and then provide my own view as to why it fails.
A key point for the critics is that Bayesians see the development of rational views on probability as a step by step matter (hence the natural metaphor of a “chain” mentioned above) so that a “prior” hypothesis is modified by a new bit of evidence or data, to become a “posterior” hypothesis. That posterior may itself be the “prior” of the next day’s further revision.
Beginning with a Peculiar Hypothesis
Econoblogger Noah Smith, in a post he calls “Bayesian Superman,” suggested that something akin to Bayesian theory is at issue in the development of the common teenage sense of invincibility.
“Suppose,” he said, that a youngster has been introduced to, or has formulated for himself, proposition (H) thus: “God is watching out for me, and has a special purpose for me alone. Therefore, God will not let me die.”
Thus, the youngster gets into various scrapes and (as many fortunate teenagers do) survives them. Every such scrape – indeed every day that passes, perhaps every moment that passes, because every moment of life contains some risk of death – may be taken as a new confirming piece of evidence of H. Each moment of survival, after all, is consistent with H. If a corollary of H were formulated as “I won’t de today,” then the sight of a sunset is confirmation. It is, then, “totally and completely rational, at least by [Noah Smith’s reading of] the Bayesian definition of rationality,” that anyone who starts out with H should gain increasing confidence in H with each passing day.
Smith seems to have been attempting a contribution to the psychology of adolescence here, not to the debate over theories of probability. But … another blogger soon took the point and ran with it. Lars P. Syll , a professor of social studies and associate professor of economic history at Malmo University, decidedly does believe that the thought experiment proves something about probability theory. What it proves, to his mind, is that though Bayesianism is mathematically unquestionable (that is, internally coherent), it is inapplicable to real world situations, and scientists should have no truck with the stuff. For them, Bayesianism is a “dangerous religious” that threatens harm.
In this connection Syll quotes yet another blogger, Andrew Gelman, who says that for scientists Bayesianism represents a dead end, and that for statisticians it represents a withdrawal from “the deeper questions of inference.”
On Tuesday afternoon, Smith acknowledged Syll’s point in a tweet: “My ‘Bayesian Superman’ post wasn’t a knock on Bayesianism, but this Andrew Gelman essay does raise some good points,” – with a link to Syll, and thus to the Gelman quote there.
Have They Taken Bayes Down?
I think not. The phrase that first comes to mind reading up on this line of attack is “survivorship bias.” As we have often observed at AllAboutAlpha, only the hedge funds that survive continue to report performance figures.
Likewise, only those who have not yet died can be said to draw any inferences at all, Bayesian or otherwise. Someone who has died doesn’t then have the luxury of saying, “Aha! Now I know there is a zero probability of H!”
Smith notices and mentions the survivorship issue, then waves his hands around a bit.
On a closely related point, I have to expect that Bayes, and any non-cartoonish Bayesian, would have a difficulty with a hypothesis that can only be stated with the use of the pronoun “I” or “me.” Certainly lemming #3 can notice that his friends, lemmings #1 and #2, both died after jumping off a cliff, and this observation should decrease in the mind of any rational lemming the plausibility of any hypothesis that makes the act of jumping off a cliff seem a safe one. The fact that ##1 and 2 can no longer be aware of this inference shouldn’t keep #3 from drawing it.
Whatever one’s take on Clark Kent or teenagers, one needn’t infer that Smith’s thought experiment makes much of a dent in the case for a Bayesian understanding of probability, under any non-parodic understanding of the latter.



